TL;DR: Scaling the input features, causes the gradient of the cost to converge faster.
Introduction
While running a machine learning experiment using linear regression, I noticed that the batch gradient descent algorithm converges faster when the data is scaled. Since, we know the effects of scaling helps in models like KNN where the magnitude of each observation plays a very important role, but why is convergence affected in case of batch-gradient descent? Why was scaling having such a big impact? In the experiment if I do not scale the features the algorithm does not converge in a fixed number of steps. After scaling, the algorithm converges in half the number of steps initially used! First, let’s look at the cost function that is in this experiment.
Cost function
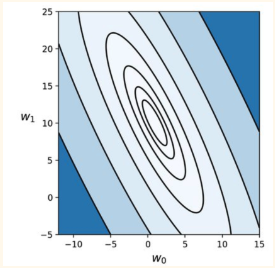
I used residual sum of squares error as the cost function in this experiment. Rss = ((theta_0 + theta_1*x) - y )^2 This will give us an ellipse equation. But if we scale our input value (x) such that the values are between 0 and 1. The equation smooths to look like a circle, when the equation is plotted with theta_0 on the x-axis and theta_1 on the y_axis. Moving forward, remember how scaling the input smooths the contour.
How do gradients work?
The gradient of a multivariate function gives us the direction where the function increases the fastest and its magnitude gives us the rate of increase. For a more intuitive example, think of burning an incense stick and then observing its smoke. In three dimensional space the smoke will move in one direction(xmax, ymax, zmax) faster as compared to other directions, and that is the gradient!
Use of Gradients in Machine Learning
All the parametric models in machine learning have a cost function. We try to find the minima of that cost function as we want our model to learn the relationship between our input data and the output label. With the help of gradients we know how to calculate the direction of fastest increase in function. We use this technique to get the direction in which the cost of our system increases the most and then move in the opposite direction. Why the opposite? Because we want to reach the minimum point of this increasing function. Why the minimum? The minimum point will give us the minimum cost!
Gradient of an ellipse vs circle
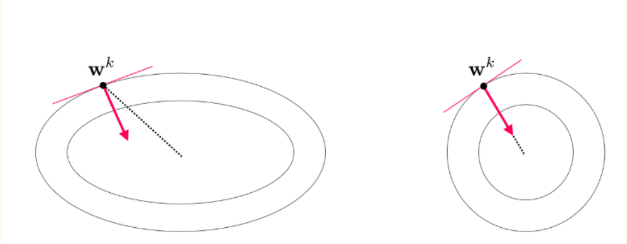One of the things we should remember in order to understand why scaling is required is that the gradient of an ellipse does not point to its center, whereas in the case of a circle the gradient will always point to the center. At the center lies the point where the cost is minimum.
Impact of scaling
When we scale the inputs and squash the values between 0 - 1. This automatically smoothes the contours of our cost function to be more circular. Normalizing will result in a cost function with less elliptical and more 'circular' contours. This gives us two advantages, the gradient would converge faster as its natural direction would be towards the center and we could increase the step size or learning rate “alpha” in this case to reach the minima even quicker, as there would be less zig-zag movement by the gradient vector to find the minima.